図１のような、水平とのなす角がθのなめらかな斜面となめらかな鉛直面から

なる質量Mの台Aを考え、その斜面上に質量mの小物体Bをおく。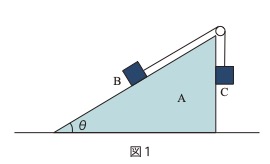

この小物体Bに軽くて伸びない糸の一端をつなぎ、それをこの斜面上端に

固定された軽くてなめらかに回る滑車に通して、そのもう一方の端に質量mの

小物体Cをつないで、小物体Cを滑車から鉛直につり下げたとき台Aの鉛直面に

接するようにする。小物体Bと滑車の間の糸は斜面に平行に保たれ、さらに

小物体BとCはいずれも台Aの上端または下端に達しないとし、また重力加速度の

大きさをg遠く。空気の影響はないものとして、次の問いに答えよ。

[A] 図１のように、台Aを水平面上に固定し、小物体B を斜面上に止めた状態から

静かにはなすと、小物体BとCは動き始めた。このとき次の問いに答えよ。

(１) 小物体Cは上昇するか下降するか。

小物体Bから糸が受ける力はmg sinθまた小物体Cから糸が受ける力はmgなので糸はC側に動く、よって下降する。

(２) 小物体Cの加速度の大きさを求めよ。

加速度α、糸の張力をTとして運動方程式をたてると、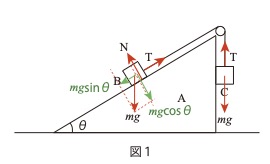

小物体Bについての運動方程式は

mg−T=mα 　①式

小物体Cについての運動方程式は

T−mg sinθ=mα　②式

①式＋②式よりmg(1-sinθ)＝２mαしたがって

α＝g(1-sinθ)/2

(３) 糸が小物体Bを引く力の大きさを求めよ。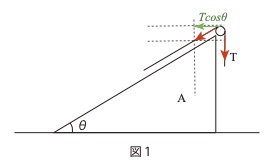

②式−①式より２T−mg−mg sinθ＝０したがって

T=mg(1+ sinθ)/2

(４) 糸が滑車を通して台Aを押す力の水平方向の成分の大きさを求めよ。

T cosθなのでmgcosθ(1+ sinθ)/2

 

[B] 図２のように、台Aをなめらかな水平面上に置き、それを水平に一定の力で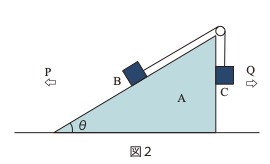

引くことにより等加速度運動をさせると、小物体Bが斜面上のある位置に止まった

ままになった。このとき次の問いに答えよ。

(１) 台Aを引く力の向きは、図２の矢印PとQのいずれの向きか。

Bに斜面に平行な下向きの力が働けば良いのでBにPの方向の慣性力が働けば良い。よってQの方向

(２) 台Aの加速度の大きさを求めよ。

慣性力をIとすると斜面に平行な下向きの力は　I cosθ＋mg sinθこれが張力Tとつりあえば良いので

　I cosθ＋mg sinθ=T　Bが台Aに対して静止している状態ではT=mgであるので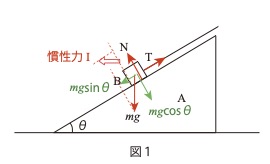

I cosθ=mg-mg sinθ=mg(1- sinθ)したがってI=mg(1- sinθ)/cosθこのときの加速度はg(1- sinθ)/cosθ

(３) 小物体Bが台Aから受ける抗力の大きさを求めよ。

mg cosθ−I sinθ

＝mg cosθ−mg(1- sinθ) sinθ/cosθ＝{mg cos2θ-mg sinθ+mg sin2θ}/cosθ

=mg(1- sinθ)/cosθ

(４) 台Aを引く力の大きさを求めよ。

台Aと小物体BCが一体となっているのですから

(M+2m)g(1- sinθ)/cosθ

[C] 台Aがなめらかな水平面上を自由に動くことができるようにする。

さらに図３のように小物体Cの右側になめらかな鉛直の壁Dを台Aに固定し、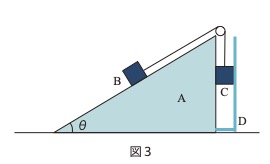

小物体　Cが台Aの鉛直面に接しながら台Aに対し上下にのみなめらかに

動くようにする。この状況で、小物体Bをその斜面上で動かないように支え、

かつ、台Aを水平面上で動かないように支える。この状態から台Aと小物体Bの支えを同時に静かに外すと、台Aおよび小物体B

とCは動き始めた。台Aに取り付けた壁Dからなる部分の質量はないものとして。次の問いに答えよ。

(１) 台Aの加速度の大きさをαA、また台Aに対して静止した(台Aとともに動く)観測者から見たときに、小物体C が鉛直方向に動く加速度の大きさをαCとするとき、加速度の大きさの比αC/αAをM,m,θを用いて表せ。

まず運動の方向を明確にしよう。系全体の重心の位置は変わらないから、小物体Bが右に移動するので重心は右に移動する。

重心は移動しないので系全体は左に移動する。これに基づいてそれぞれに働く力を図示すると。

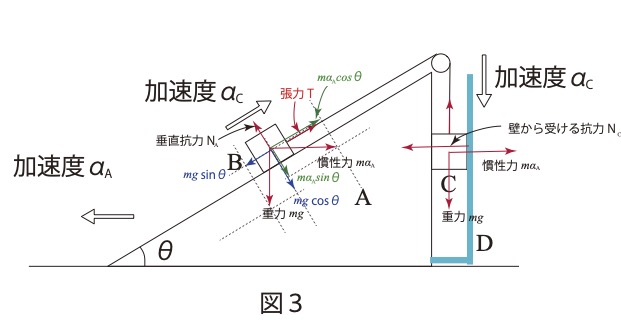
小物体Bについての運動方程式は

①

小物体Bの斜面に垂直な方向のつりあいの式は

②

小物体Cについての運動方程式は

③

小物体Cについての水平方向のつりあいの式は

④

台Aに働く力を図示すると

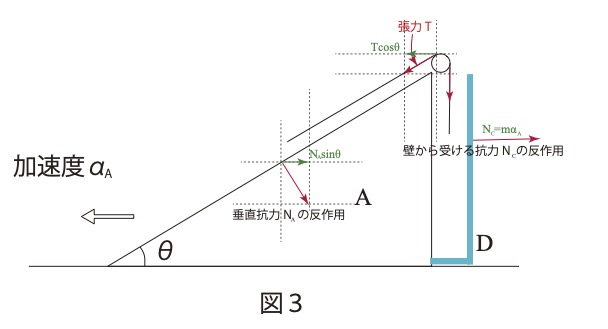
台Aについての運動方程式は

⑤

①より　これと②式を⑤に代入すると

展開して整理すると

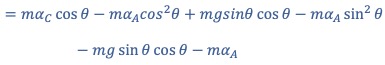
よって

(２) αCをM,m,g,θを用いて表せ。

①、③式より

となります。

（大分理系専門塾WINROAD 首藤）