図１に示すように直交座標系を設定する。

初速度の無視できる電荷q (q>0)、質量m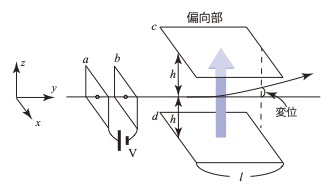

の電子が、y軸上で小さな穴のある電極a

の位置から電極a, b 間の電圧Vでy軸の

正の向きに加速され、z軸に垂直でy軸方

向の長さがlの平板電極c、d (z=±h) から

なる偏向部に入る。c , d間にはz軸の正の

向きに強さEの一様な電場(電界)が加えられている。これらの装置は真空中にある。

電場は平板電極c、dにはさまれた領域の外にはもれ出ておらず、ふちの近くでも電極に

垂直であるとし、地磁気および重力の影響は無視できるとする。

[A] 電場bの穴を通過した瞬間の陽子の速さ​\( v_0 \)​をV、q、mを用いて表せ。

エネルギー保存則より​\( qV=\dfrac{1}{2}m{v_0}^2 \)​

よって​\( v_0=\sqrt{\dfrac{2qV}{m}} \)​

[B] その後、陽子は直進し、速さ​\( v_0 \)​のままで偏向部に入る。

(1) 陽子が電極cに衝突することなく偏向部を出る場合、その瞬間のz座標(変位)​\( z_1 \)​を、

​\( v_0 \)、q、m、l、Eを用いて表せ。

偏向部では陽子に電場から上向きにq Eの力を受けるので上向きに​\( \dfrac{qE}{m} \)​の

加速度を生じる。偏向部を通過するのにかかる時間は​\( \dfrac{l}{v_0} \)​

​\( z_1=\dfrac{1}{2}\dfrac{qE}{m}(\dfrac{l}{v_0})^2=\dfrac{qEl^2}{2m(v_0)^2} \)​

(2) Eがある値E1より大きければ陽子は電極cに衝突し、小さければ衝突しない。その

値E1をV、l、hを用いて表せ。

​\( \dfrac{qE_1l^2}{2m(v_0)^2}=h \)​とおくと​\( E_1=\dfrac{2mh}{ql^2}(v_0)^2=\dfrac{2mh}{ql^2}\dfrac{2qV}{m}=\dfrac{4hV}{l^2} \)​

[C] 陽子のかわりにα粒子(電荷２q、質量4m)を用いて同じV、Eの値で実験を行ったところ

偏向部を出る瞬間のz座標(変位)は​\( z_2 \)​であった。​\( z_2 \)​を​\( z_1 \)を用いて表せ。

まず加速部通過後の速さを​\( v_\alpha \)​とするとエネルギー保存則より

​\( 2qV=\dfrac{1}{2}4mv_\alpha{}^2 \)​より​\( v_\alpha=\sqrt{\dfrac{qE}{m}}=\dfrac{v_0}{\sqrt{2}} \)​

偏向部を通過するのにかかる時間は​\( \dfrac{l}{v_\alpha}=\dfrac{\sqrt{2}\ l}{v_0} \)​

偏向部ではα粒子に​\( 2qE \)​の上向きの力が働くので受ける加速度は​\( \dfrac{2qE}{4m}=\dfrac{qE}{2m} \)​

よって​\( z_2=\dfrac{1}{2}\dfrac{qE}{2m}(\dfrac{\sqrt{2}\ l}{v_0})^2 =\dfrac{qEl^2}{2m(v_0)^2}=z_1\)​

つまり​\( z_2=z_1 \)​

[D] Eの値を​\( E_1 \)​に固定し、電極c、dにはさまれた領域にx軸の正の向きに磁束密度B(​\( B>0 \)​)の

一様な磁場(磁界)を加え、再び陽子を用いて実験した。

(1) Bをある値​\( B_1 \)​にしたところ、陽子は偏向部を直進し、偏向部を通過するのに時間​\( T_1 \)​を

要した。​\( B_1 \)​と​\( T_1 \)​を、​\( v_0 \)​、​\( E_! \)​、lを用いてそれぞれ表せ。

陽子は磁場によって下向きに​\( qv_0B_1 \)​の力を、電場によって上向きに\( qE_1 \)​の力を受けるので

これがつりあい陽子は直進する。

よって​\( qv_0B_1=qE_1 \)​つまり​\( B_１＝\dfrac{E_1}{v_0} \)​

通過時間は​\( T_1=\dfrac{l}{v_0} \)​

(2) Bをある値​\( B_2 \)​(​\( 0<B_2<B_1\))にしたところ、陽子が偏向部を出る直前のz座標(変位)は

​\( z_3 \)​(​\( z_3>0 \)​)であった。このときの陽子の速さ​\( v_1 \)​を、q、m、V、​\( E_1 \)​、​\( z_3 \)​を用いて表せ。

まず磁場は陽子の進行方向に対して常に垂直な向きに力を働かせる。つまり陽子に対して仕事をしない、

ところが電場は上向きに​\( qE_1 \)​の力、その向きに​\( z_3 \)​変位しているので

陽子に対してした仕事は​\( qE_1z_3 \)​エネルギー保存則より

​\( \dfrac{1}{2}m(v_0)^2++qE_1z=\dfrac{1}{2}m(v_1)^2 \)​より

​\( v_1=\sqrt{(v_0)^2+\dfrac{2qE_1z_3}{m}} \)​

ここで​\( v_0=\sqrt{\dfrac{2qV}{m}} \)​なので

​\( v_1=\sqrt{(v_0)^2+\dfrac{2qE_1z_3}{m}}=\sqrt{(\sqrt{\dfrac{2qV}{m}})^2+\dfrac{2qE_1z_3}{m}}=\sqrt{\dfrac{2q}{m}(V+E_1Z_3)} \)​

(3) Bを​\( 0<B​<B_1\)の範囲内で変化させて実験を繰り返し。陽子が偏向部を通過するのに

要する時間Tを測定した。このとき、BとTの関係を表すグラフはどのようになるか。

図の(ア)〜(オ)の中から最も適当なものを１つ選べ。

​\( B=0 \)​のときは​\( T=\dfrac{l}{v_0} \)​、​\( B=B_1 \)​のとき[D]の(1)より​\( T_1=\dfrac{l}{v_0} \)​

これにより選択肢は(ア)、(イ)、(オ)となります。

さらに偏向部の通過時には進行方向に対して垂直に磁場から力を受け、電場から鉛直上向きに力を受ける。

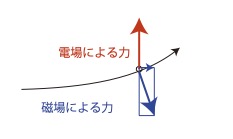
磁場による力のy軸方向の成分により加速されるので、通過時間は

短くなる。よって(ア)となります。

 

 

 

（大分理系専門塾WINROAD 首藤）