問題

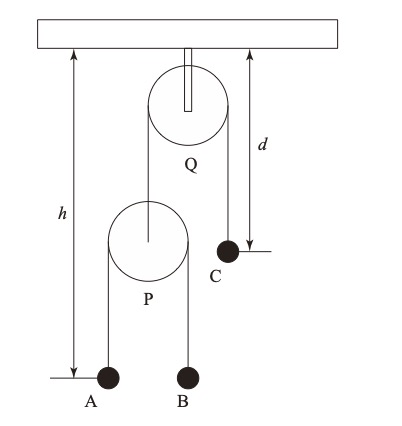
図に示すように、質量M[kg]の小さい

おもりAと、質量３M[kg]の小さいおも

りBを糸で結び、なめらかな滑車Pに

かける。さらに、この滑車Pと小さい

おもりCを糸で結び、天井からつって

あるなめらかな滑車Qにかける。滑車と

糸の重さは無視し重力の加速度は

g[m/s²]として以下の問いに答えなさ

い。

A,B,Cを固定しA ,B,Cを全部同時に静かに

はなす。

(a) いま、Cの質量が４M[kg]であるとき、A,Bの質量の和がCの質量に等しいのにもかかわらず、Cは

動き始める。

(ア) Cの加速度の大きさはいくらか。

(イ) AとBを結ぶ糸の張力はいくらか。

(ウ) AとBは、はじめ、天井からの距離h[m]の同じ高さに、Cは天井からの距離d[m]の高さにあった

とする。このAとBの高さの差がl[m]になるとき、AとCの位置はどうなるか。天井からの距離で示せ。

 

(b) Cが静止し続けるのは、Cの質量がいくらのときか。

---

 

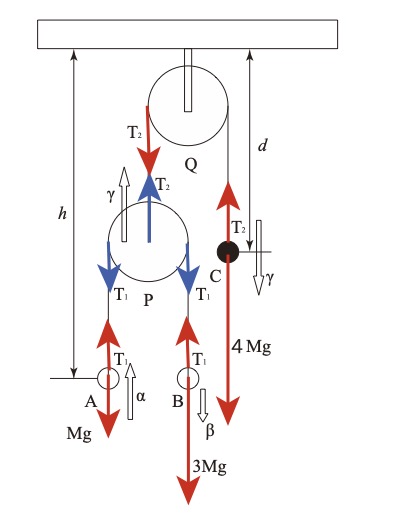
Aについての運動方程式は

​\( T_1-Mg=M\alpha\dots① \)​

Bについての運動方程式は

​\( 3Mg-T_1=3M\beta\dots② \)​

ここで滑車Pは質量が無視できるので

​\( T_2-2T_1=0・\gamma\\T_2=2T_1\dots③ \)​

Cについての運動方程式は

​\( 4Mg-T_2=4M\gamma\dots④ \)​

また滑車Pに対するAとBの相対加速度の

大きさは等しいので

​\( \alpha-(+\gamma)=\beta-(-\gamma)\\\alpha-\gamma=\beta+\gamma\dots⑤ \)​

③、④より​\( 4Mg-2T_1=4M\gamma\dots⑥ \)​

①×３ー②より​\(4T_1-6Mg=3M(\alpha-\beta)=3M(2\gamma)=6M\gamma \)​

​\( 4T_1-6Mg=6M\gamma\dots⑦ \)​

⑥×２＋⑦より​\( 2Mg=14M\gamma \)​よって​\( \gamma=\dfrac{1}{7}g \)​ (ア)

⑥より​\( 2Mg-T_1=2M\gamma⇨T_!=2Mg-2M\gamma\\=2Mg-2M\dfrac{1}{7}g=\dfrac{12}{7}Mg \)​

​\( T_1=\dfrac{12}{7}Mg \)​(イ)

①より​\( \alpha=\dfrac{T_1}{M}-g=\dfrac{12}{7}g-g=\dfrac{5}{7}g \)​

②より​\( \beta=g-\dfrac{T_1}{3M}=g-\dfrac{4}{7}g=\dfrac{3}{7}g \)​

AとBの高さの差がlになるまでの時間をtとすると。

​\( l=\dfrac{1}{2}\alpha t^2+\dfrac{1}{2}\beta t^2=\dfrac{t^2}{2}(\alpha+\beta) =\dfrac{t^2}{2}\cdot\dfrac{8}{7}g=\dfrac{4g}{7}t^2\)​

​\( t^2=\dfrac{7l}{4g} \)​

t秒後のCの位置は​\( d+\dfrac{1}{2}\gamma t^2=d+\dfrac{1}{2}\cdot\dfrac{1}{7}g\cdot\dfrac{7l}{4g}=d+\dfrac{l}{8} \)​​(ウ)

Aの位置は​\( h-\dfrac{1}{2}\alpha t^2=h-\dfrac{1}{2}\cdot\dfrac{5}{7}g\cdot\dfrac{7l}{4g}=h-\dfrac{5l}{8} \)​​(ウ)

 

滑車Pが静止しているときの張力​\( T_1 \)​は

​\( T_1-Mg=Ma\\3Mg-T_1=3Ma \)​

を解いて​\( a=\dfrac{1}{2}g \)​、​\( T_1=\dfrac{3}{2}Mg \)​

​\( T_2=2T_1 =3Mg\)​よりCが静止し続けるのは、3Mのとき。(b)

 

 

（大分理系専門塾WINROAD 首藤）