問題　​\( (x^2-2x+a)^2+(x^2-2x+a)+b=0 \)​(a、bは実数の定数)を満たす実数xは

ちょうど２個あり、そのうちの１つだけが​\( 0<x<1 \)​である。

このとき点(a、b)の存在する範囲を図示せよ。

---

まずは​\( t=x^2-2x+a \)​と置き換えることは皆考えることでしょう。

置き換えると​\( t^2+t+b=0 \)​となります。

ここで、もう少し考えます。

​\( t^2+t+b=0 \)​は２次方程式なので次の３つのような解が考えられます。

１) 異なる二つの実数解α、βを持つ。

２）重解γを持つ。

３）異なる２つの虚数解を持つ。

題意から3)は考えなくてもよいでしょう。

まず１)の場合

\( \alpha=x^2-2x+a \)​および\( \beta=x^2-2x+a \)​となります。

実数xがちょうど２個ということから片方が異なる２つの実数解を持ち

もう片方が虚数解を持つということになります。

ではもう少し、

 

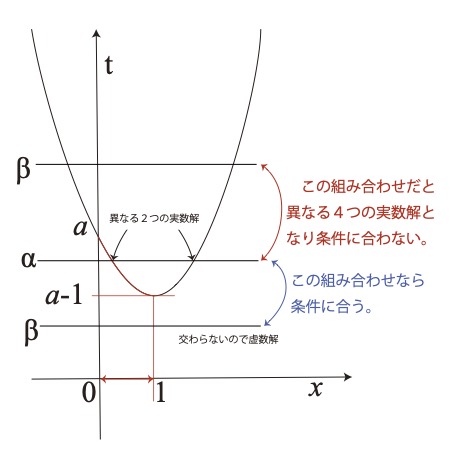
図のように１）を満たすのは

​\( a-1<t<a\)​でtが１つ定まり

​\( t＜a-1 \)​でtがもう一つ定まる事

となります。

つまり２次方程式

​\( t^2+t+b=0 \)​が

​\( a-1<t<a\)​の範囲と

​\( t＜a-1 \)​の範囲で

１つずつ解を持てば良いのです。

 

 

これは図で表すと

 

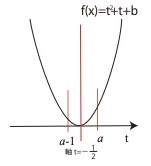のようになり。

​\( \begin{cases}f(a-1)<0\\f(a)>0\end{cases} \)​

​\( \begin{cases}(a-1)^2+(a-1)+b<0\\a^2+a+b>0\end{cases} \)​

​\( \begin{cases}b<-(a-1)^2-(a-1)\\b>-a^2-a\end{cases} \)​・・・①

 

次に２）の場合

 

図のように２）を満たすのは

​\( a-1<t<a\)​でtが１つ定まり

これが重解である。

ということになります。

つまり２次方程式

​\( t^2+t+b=0 \)​が

​\( a-1<t<a\)​の範囲で

重解を持てば良いのです。

これは図で表すと

のようになり

軸がa-1とaの間にあるので

​\( a-1<-\dfrac{1}{2}\\-\dfrac{1}{2}\)

よって​\( -\dfrac{1}{2}<a<\dfrac{1}{2} \)​

​\( \begin{cases}判別式D=0\\f(a-1)>0\\f(a)>0\\ -\dfrac{1}{2}<a<\dfrac{1}{2}\end{cases}\)

​\( \begin{cases}D=1^2-4b=0つまりb=\dfrac{1}{4}\\b>-(a-1)^2-(a-1)\\b>-a^2-a\\-\dfrac{1}{2}<a<\dfrac{1}{2}\end{cases} \)​　　　・・・②

 

以上より①、②の示す範囲を図示すると次のようになります。

 

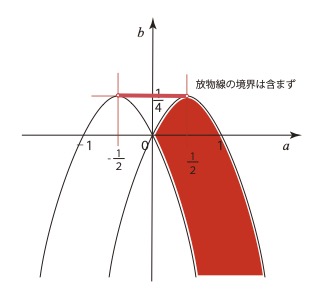
（大分理系専門塾WINROAD 首藤）