①超音波は②回折が起こりにくく指向性が高いなどの特性から、医療の画像診断や各種産業の

計測・探知機など、さまざまな用途に用いられている。

動物の中には、超音波を利用して周囲の物体までの距離や速度などを測定するものがいる。

このようなしくみをエコーロケーションという。ここでは、コウモリが行うエコーロケー

ションを考えてみよう。空気中の音の速さはV[m/s]で、空気の温度は一定で無風であるとする。

また、音速の減衰や透過は無視する。

(1)　赤字の部分①、②の語句の意味を説明せよ。

①超音波：　人が聞き取ることができない高い振動数の音(人が聞き取ることができる

　　　振動数は20Hz〜20000Hz)

②回折　：　波が障害物の背後まで回り込んで伝わる現象

図１のように、静止したコウモリが平らな崖に向けて振動数f[Hz]の超音波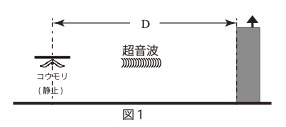

を発した。超音波は崖に当たって反射し、コウモリが超音波を発してから

最初に反射波を聞くまでの時間はt[s]であった。

(2)　この超音波の周期と波長をそれぞれ求めよ。

、となります。

(3)　コウモリから崖までの距離D[m]を求めよ。

となります。

図２のように静止したコウモリが崖に止まった昆虫に向けて振動数fの

超音波を発した。超音波は昆虫の表面と崖の表面で反射した。次に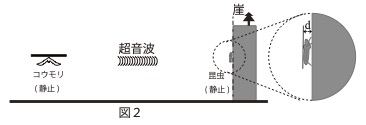

コウモリが超音波の振動数をfから徐々に低下

させると、振動数がf0[Hz]のとき反射波が最も

弱まったが、振動数をf0より低くすると反射波

が弱まることはなかった。ここでは、昆虫の表面と崖の表面で反射のしかたに違いはなかったものと

する。

(4)　反射波が弱まった理由を説明せよ。

昆虫の表面で反射した反射波と崖の表面で反射した反射波が干渉し弱めあったため。

(5)　この昆虫の厚さd[m]を求めよ。

距離の差がλ/2の奇数倍になれば良い。「振動数をfから徐々に低下させると、振動数がf0[Hz]のとき

反射波が最も弱まった」とあるので距離の差がλ/2になれば良い

となります。

図３のように、コウモリが昆虫に向かってまっすぐに

一定の速さv[m/s]で飛び、その向きへ静止時と同じ

振動数fの超音波を時間Δt[s]にわたり発した。

昆虫はコウモリに向かってまっすぐに一定の速さw[m/s]で飛んできた。

(6)　時間Δt内にコウモリの発した超音波の振動の回数を求めよ。

1秒でf 回なのでf・Δt回となります。

(7)　時間Δt内にコウモリの発した超音波の空気中での長さL[m]を求めよ。

Δt秒で超音波はVΔt進む、この間コウモリはvΔt進んでいるのでL=VΔt−vΔt＝(V−v)Δtとなります。

(8)　コウモリの発した超音波の空気中での波長を求めよ。

Δt秒で fΔt回振動しているので

その後、この超音波は昆虫に当たって反射し、コウモリがその反射波を聞くと、

コウモリはうなりを感じた。

(9)　昆虫が受ける超音波の振動数を求めよ。

観測者と音源が互いに向かって進むドップラー効果なので

(10)　コウモリが感じた単位時間当たりのうなりの回数を求めよ。

昆虫が振動数f’の超音波を反射しながらコウモリに向かって近づくので

コウモリが聞く反射波の振動数はなので

うなりの回数は

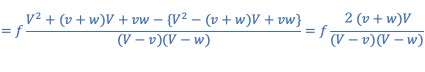となります。

（大分理系専門塾WINROAD 首藤）