次の文中の空欄 [ ア ]〜[ ク] に当てはまる式を記せ。
ただし、重力加速度の大きさを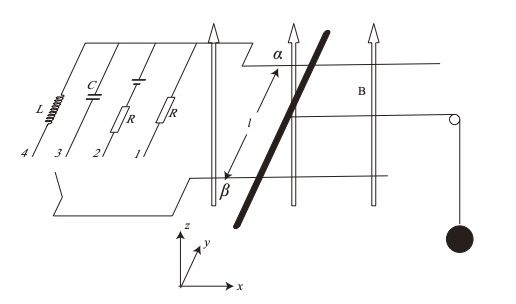
g[\( m/s^2 \)]とする。
図のように、鉛直上向きの磁束密度
B[T]の一様な磁場中に、長い2本の
導線が平行に間隔 l [m]をおいて
水平に置かれている。導線に
そって x 軸、水平面内で導線に
垂直な向きに y 軸鉛直上向きに z 軸をとる質量 m[kg]の導体棒を2本の導線をまたいで y 軸に平行に置き、
滑車を通して質量M[kg]のおもりを軽い糸でつりさげる。導体棒は y 軸に平行な向きを
保ったまま x 軸方向に運動する。導線の幅αーβ間に抵抗値R[Ω]の抵抗、電池、
電気容量C[F]のコンデンサー、自己インダクタンスL[H]のコイルを切り替えて
接続できるスイッチがついている。滑車の軸、滑車と糸、および導線と導体棒との
間の摩擦と、電池の内部抵抗は無視できる。また、コンデンサーには初めに電荷は
たくわえられていないものとする。
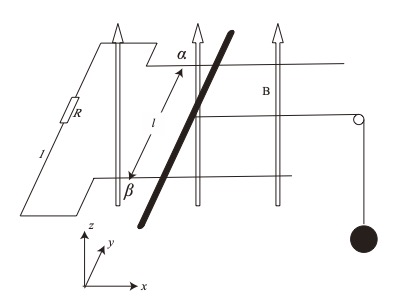
導体棒を手で支えて静止させた状態で、スイッチで端子1を選び、抵抗に接続した。
静かに手を離すと、導体棒は導線の上をすべり始めた。導体棒の速さが v [m/s]のとき、
導体棒を流れる電流の大きさは [ ア ] [A]である。十分に時間がたったのち、導体棒は
一定の速さ [ イ ] [m/s]で運動する。
この場合導体棒に生じる起電力はvBl [V]なので
電流の大きさは\( \dfrac{vBl}{R} \)[A] [ ア ]となります。
導体棒が速さvで移動するとき
\( \dfrac{vBl}{R} \)[A]の電流が流れます。
その向きは導体棒中をαからβの向きです。
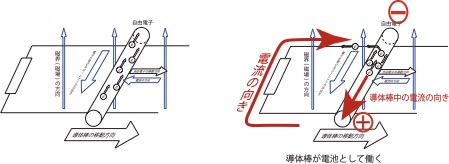
これにより導体棒は左向きに力を受けます。これと
糸が棒を引く力がつり合って加速度を生じない一定の
速さとなります。
つりあいの式から\( IBL=Mg\\\dfrac{vBl}{R}Bl=Mg \)
よって\( v=\dfrac{MgR}{(Bl)^2} \) [ イ ] [m/s]となります。
スイッチで端子2を選び、電池と抵抗に接続した。十分に時間がたった後、おもりを一定の速さ
\( v_0 \)[m/s]で引き上げるために必要な電池の電圧は [ ウ ][V]である。おもりが一定の速さ
\( v_0 \)で運動するようになったのち、導体棒がh [m]だけ移動する間に電池がした仕事は
[ エ ] [ J ]である。
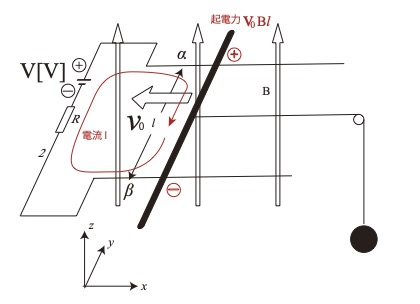
この回路でキルヒホッフの法則を用いる
\( V-v_0B\mathit{l}-IR=0 \)なので
\( I=\dfrac{V-v_0Bl}{R} \)
これによって生じる力と糸の張力が
つり合うので
\( IB\mathit{l}=\dfrac{V-v_0Bl}{R}Bl=Mg \)
よって\( V=v_0Bl+\dfrac{MgR}{Bl} \) [ ウ ][V]となります。
このとき\( I=\dfrac{v_0Bl+\dfrac{MgR}{Bl}-v_0Bl}{R}=\dfrac{Mg}{Bl} \)
h引き上げるのにかかる時間は\( t=\dfrac{h}{v_0} \)なので電池がした仕事は
\( W=Vit=\left(v_0Bl+\dfrac{MgR}{Bl}\right)\dfrac{Mg}{Bl}\dfrac{h}{v_0}=Mgh+\dfrac{(Mg)^2Rh}{(Bl)^2v_0} \)
\( =Mgh\left(1+\dfrac{MgR}{(Bl)^2v_0}\right) \)[ エ ] [ J ]
導体棒を手で支えて静止させ、スイッチで端子3を選びコンデンサーに接続した。
静かに手をはなしたところ、おもりは下降し、導体棒は一定の加速度で運動しはじめた。
導体棒の加速度の大きさは[ オ ] [\( {m}/{s^2} \)]である。
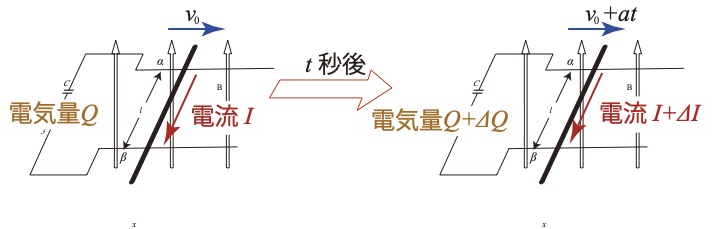
ある瞬間の導体棒の速さが\( v_0 \)であるとしてt秒後について考える。
このときの加速度をa [\( m/s^2 \)]とすると、
導体棒の速さは v0+at [m/s]、誘導起電力は (v0+at)Bl、流れた電流はΔI、
コンデンサーに流れた電気量はΔQ、
\( Q=Cv_0Bl \)。\( Q+ΔQ=C(v_0+at)Bl \)、\( ΔQ=(Q+ΔQ)-Q=C(v_0+at)Bl -Cv_0Bl=CatBl\)
\( ΔI=\dfrac{ΔQ}{t}=\dfrac{CatBl}{t}=CaBl \)
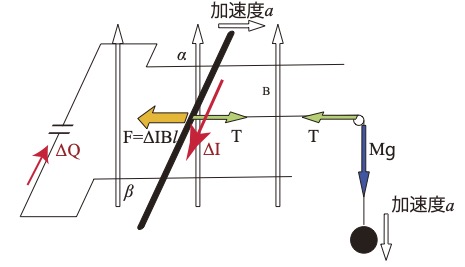
運動方程式を立てると
導体棒\( T-ΔIBl=ma \)
おもり\( Mg-T=Ma \)
\( Mg-(ma+ΔIBl)=Ma\\Mg-ma-Ca(Bl)^2=Ma\\Mg=(M+m+C(Bl)^2)a\\a=\dfrac{Mg}{M+m+C(Bl)^2} \)
\( \dfrac{Mg}{M+m+C(Bl)^2} \) [ オ ] [\( {m}/{s^2} \)]
導体棒を手で支えて静止させ、スイッチで端子4を選び、コイルに接続した。
コイルを流れる電流が0の状態で、静かに手をはなした。短い時間Δt [ s ]の間に、
導体棒の位置がΔx [ m ]だけ変化し、コイルを流れる電流がΔI [ A ]だけ変化したとすると、
\( \mathit{|ΔI|=} \)[ カ ] \( \times|Δ\mathit{x}| \)と表せる。導体棒には復元力が
働き、導体棒は角振動数[ キ ] [rad/s]、振幅[ ク ] [ m ]で単振動する。
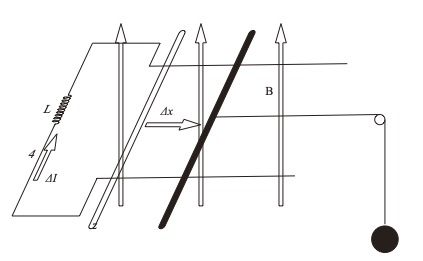
このとき導体棒に生じる起電力は
\( vBl=\dfrac{Δx}{Δt} \ Bl \)
また、コイルに生じる誘導機電力は
\( -L\dfrac{ΔI}{Δt} \)
\( \dfrac{Δx}{Δt}\ Bl-L\dfrac{ΔI}{Δt}=0 \)
\( \dfrac{Δx}{Δt}\ Bl=L\dfrac{ΔI}{Δt}\\ΔI=\dfrac{Bl}{L}\ Δx \)
\( \dfrac{Bl}{L} \)[ カ ] \( \times|Δ\mathit{x}| \)となります、\( I=\displaystyle\int\dfrac{Bl}{L}dx=\dfrac{Bl}{L}x+C(cは積分定数) \)
\( x=0のときI=0より \)\( C=0 \)よって\( I=\dfrac{Bl}{L}x \)
このとき導体棒に働く力は糸の張力と張力とは逆向きの\( IBl=\dfrac{Bl}{L}xBl=\dfrac{(Bl)^2}{L}x \)
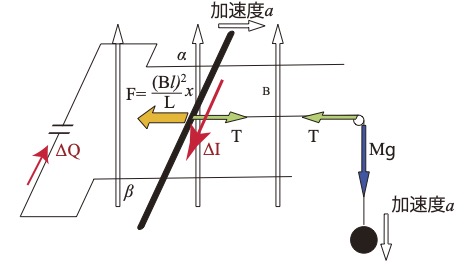
導体棒とおもりの運動方程式は
\( T-\dfrac{(Bl)^2}{L}\ x=mα\\Mg-T=Mα \)
Tを消去すると。
\( Mg-(mα+\dfrac{(Bl)^2}{L}x)=Mα\\(M+m)α=Mg-\dfrac{(Bl)^2}{L}x \)
\( α=\dfrac{1}{(M+m)}(Mg-\dfrac{(Bl)^2}{L}x)\\=-\dfrac{(Bl)^2}{(M+m)L}(x-\dfrac{MgL}{(Bl)^2}) \)
\( α=ーω^2\ x単振動 \)なので
\( ω^2=\dfrac{(Bl)^2}{(M+m)L}\) \( ω=\dfrac{Bl}{\sqrt{(M+m)L}} \)[ キ ] [rad/s]
求めた式から振動の中心は\( \dfrac{MgL}{(Bl)^2} \)なので\( x=0 \)からの距離が振幅となります。
したがって振幅は\( \dfrac{MgL}{(Bl)^2} \)[ ク ] [ m ]
(大分理系専門塾WINROAD 首藤)