問題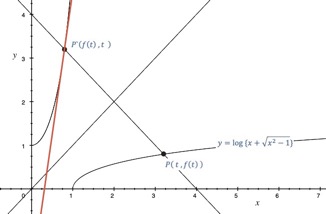
関数\( f(x)=log(x+\sqrt{x^2-1}) \)\( (x\geqq0) \)の
逆関数を\( g(x) \)とする。
\( y=g(x) \)上の点\( P(f(t)、t) \)における接線を求めよ。
関数
\( f(x)=log(x+\sqrt{x^2-1}) \)\( (x\geqq0) \)
上で、点Pに対応する点P’は
\( P'(t、f(t)) \)
でこの点における接線の方程式は
\( y-f(t)=f'(t)(x-t) \)
です。
この接線の逆関数が
\( P'(t、f(t)) \)
における の接線となります。
つまり、求める接線の方程式は
\( y-f(t)=f'(t)(x-t) \)
のxとyを入れ替えた
\( x-f(t)=f'(t)(y-t) \)
となります。つまり
\( f'(x)=\dfrac{(x+\sqrt{x^2-1})’}{x+\sqrt{x^2-1}}=\dfrac{1}{x+\sqrt{x^2-1}}\left(1+\dfrac{1}{2}\dfrac{2x}{\sqrt{x^2-1}}\right)=\dfrac{1}{\sqrt{x^2-1}} \)
なので
\( x-log(t+\sqrt{t^2-1})=\dfrac{1}{\sqrt{t^2-1}}(y-t) \)
\( y-t=\sqrt{t^2-1}(x-log(t+\sqrt{t^2-1}) \)
\( y=\sqrt{t^2-1}\cdot{(x-log(t+\sqrt{t^2-1})}+t \)
\( y=\sqrt{t^2-1}\cdot{x}-\sqrt{t^2-1}log(t+\sqrt{t^2-1})+t \)‥‥‥①
となります。
ここで逆関数を求めてから接線を求めてみます。
\( y=log(x+\sqrt{x^2-1}) \)
の逆関数はxとyを入れ替えて
\( x=log(y+\sqrt{y^2-1}) \)
つまり
\( y+\sqrt{y^2-1}=e^x \)
両辺をxで微分すると
\( 1+\dfrac{1}{2}\cdot{\dfrac{2y}{\sqrt{y^2-1}}}\cdot{\dfrac{dy}{dx}}=e^x \)
まとめると\( e^x=\dfrac{y+\sqrt{y^2-1}}{\sqrt{y^2-1}}\cdot{\dfrac{dy}{dx}} \)
\( f'(x)=\dfrac{dy}{dx}=\dfrac{e^x\sqrt{y^2-1}}{y+\sqrt{y^2-1}} \)
ここで
\( P(f(t)、t) \)における接線の傾きは上の式の
xとyに\( x=f(t) \)、\( y=t \)を代入し
\( f'(f(t))=\dfrac{e^{f(t)}\sqrt{t^2-1}}{t+\sqrt{t^2-1}}=\dfrac{e^{log(t+\sqrt{t^2-1})}\sqrt{t^2-1}}{t+\sqrt{t^2-1}}=\dfrac{(t+\sqrt{t^2-1})\sqrt{t^2-1}}{t+\sqrt{t^2-1}} \)
\( =\sqrt{t^2-1} \)となります。
だから接線の方程式は
\( y-t=\sqrt{t^2-1}(x-f(t)) \)
\( y-t=\sqrt{t^2-1}(x-log(t+\sqrt{t^2-1})) \)
\( y=\sqrt{t^2-1}\cdot{x}-\sqrt{t^2-1}log(t+\sqrt{t^2-1})+t \)となり①と同じになります。
逆関数の取り扱いは元の関数との関係をしっかりみて、元の関数をうまく利用しましょう。
(大分理系専門塾WINROAD 首藤)