2次関数の面積公式
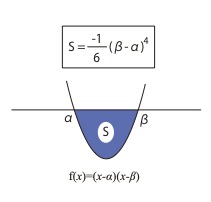
\( \displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=-\dfrac{1}{6}(\beta-\alpha)^3 \)
x軸より下の部分の面積なので積分結果は負の値になります。
純粋に面積という事なら絶対値をとった値となります。
\( 面積=\dfrac{1}{6}(\beta-\alpha)^3 \)
3次関数の面積公式
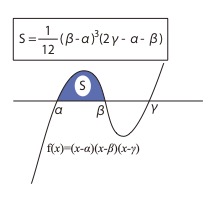
\( S=\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)(x-\gamma)dx=\dfrac{1}{12}(\beta-\alpha)^3(2\gamma-\alpha-\beta) \)
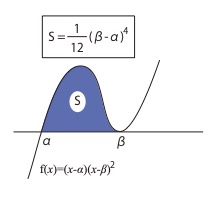
\( S=\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)^2dx=\dfrac{1}{12}(\beta-\alpha)^4 \)
(大分理系専門塾WINROAD 首藤)