熱の一部を力学的な仕事に変換する装置を熱機関という。
ある状態の気体がいくつかの異なる状態を経てもとの状態に
もどる変化はサイクルとよばれる。
いま、物質量nの単原子分子理想機体が状態Aから状態B、
状態C、状態Dと変化し、もとの状態Aにもどるサイクルで
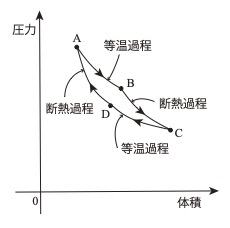
動作する熱機関Iを考える。図にこのサイクルの圧力-体積
グラフを実線で示す。状態Aから状態B、および状態Cから
状態Dの過程は等温変化であり、状態Bから状態C、および
状態Dから状態Aの過程は断熱過程である。
状態Aにおける圧力をPA、体積をVA、状態Aから状態Bにおける絶対温度をTAB、状態Cから
状態Dにおける絶対温度をTCDとする。気体定数をRとする。
[A] 状態Aから状態Bを経て状態Cに至る過程を考える。状態Bにおける体積をVB、
状態Cにおける体積をVCとする。
(1) 状態Bにおける圧力をPBとするとき、PBをPA、VA、VBを用いて表せ。
状態Aから状態Bの過程は等温過程なのでPV=一定
よってPAVA=PB VBしたがって\( P_B=\dfrac{P_AV_A}{V_B} \)
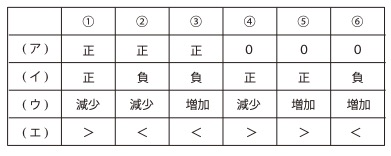
(2) 状態Bにおける温度TABと状態Cにおける温度TCDの間の関係について述べた
次の文章の(ア)〜(エ)に入る語句や記号の組み合わせとして正しいものを、
下表の①〜⑥から選び、記号でおたえよ。
「状態Bから状態Cに至る断熱過程では、気体が得る熱量は(ア)であり、
機体が外部にする仕事は(イ)であるから、内部エネルギーは(ウ)する。
よってTAB(エ)TCDとなる。
断熱過程なので熱の出入りはない。よって(ア)は0
体積が増加しているので外部にする仕事は正 (イ)は正
熱の出入りがなく外部に仕事をするので内部エネルギーは減少する。
よって(ウ)は減少
PVグラフでは双曲線が原点から遠いほど温度は高くなるので\( T_{AB}>T_{CD} \)
(エ)は>
以上より④
(3) この過程(状態A⇨状態B⇨状態C)における気体の内部エネルギーの変化量ΔUを
n、R、TAB、TCDを用いて表せ。ただし、内部エネルギーが増加する場合、
ΔU>oであるとする。
まず状態A⇨状態Bでは等温過程なので内部エネルギーは変化しない。ΔUAB=0
状態B⇨状態Cでは
\( △U_{BC}=\dfrac{3}{2}nR△T=\dfrac{3}{2}nR(T_{CD} -T_{AB})\)
ここで\( T_{AB}>T_{CD} \)より
\( △U_{BC}=-\dfrac{3}{2}nR(T_{AB} -T_{CD})\)
\( △U= △U_{AB}+ △U_{BC}=-\dfrac{3}{2}nR(T_{AB} -T_{CD})\)
(4) 断熱過程では、圧力Pと体積Vとの間には、単原子分子理想気体の比熱比を\( \dfrac{5}{3} \)として
「\( PV^\dfrac{5}{3}=一定 \)」の関係が成り立つ、この関係式を用いて、\( V_C \)の\( V_B \)に
対する比を\( \dfrac{V_C}{V_B} \)を\( T_{AB} \)、\( T_{CD} \)を用いて表せ。
まず\( P_B{V_B}^{\dfrac{5}{3}}=P_C{V_C}^{\dfrac{5}{3}} \)
気体の状態方程式から
\( P_BV_B=nRT_{AB}\\P_CY_C=nRT_{CD} \)より
\( P_B=\dfrac{nRT_{AB}}{V_B} P_C=\dfrac{nRT_{CD}}{V_C} \)これらを代入し
\( \dfrac{nRT_{AB}}{V_B} {V_B}^{\dfrac{5}{3}}=\dfrac{nRT_{CD}}{V_C}{V_C}^{\dfrac{5}{3}} \)
\( T_{AB}V_B^{\dfrac{2}{3}}=T_{CD}V_C^{\dfrac{2}{3}}\\\dfrac{T_{AB}}{T_{CD}}=(\dfrac{V_C}{V_B})^{\dfrac{2}{3}} \)
よって\( \dfrac{V_C}{V_B}=(\dfrac{T_{AB}}{T_{CD}})^{\dfrac{3}{2}} \)
[B] 熱機関Iは1サイクルにおいて外部から熱量Qin(\( Q_{in}>0 \))を得て、外部に熱量Qout(\( Q_{out}>0 \))を放出し、仕事をする。
(1) 以下の各過程において気体が外部にした仕事Wを、それぞれ、n、Qin、Qout、R、TAB、TCDのうち必要なものを用いて表せ。ただし、気体が外部に仕事をした場合はW>0、気体が外部から仕事をされた場合はW<0とする。
(ア) 状態Aから状態Bへの過程において機体が外部にした仕事WAB
(イ) 状態Bから状態Cへの過程において機体が外部にした仕事WBC
(ウ) 状態Cから状態Dへの過程において機体が外部にした仕事WCD
(エ) 状態Dから状態Aへの過程において機体が外部にした仕事WDA
(ア)等温過程なので内部エネルギーの増減はない。加えた熱量の分だけ外部に仕事をするので WAB=Qin
(イ)断熱過程なので熱の出入りはなく内部エネルギーの減少分だけ外部に仕事をする。
したがって\( W_{BC}=-\dfrac{3}{2}nR\Delta T=-\dfrac{3}{2}nR(T_{CD}-T_{AB})\\=\dfrac{3}{2}nR(T_{AB}-T_{CD}) \)
(ウ) グラフから体積が減少していることから外部から仕事をされた事になる。(ア)と同様に等温過程なので内部エネルギーの増減はない。つまり放出した熱量の分だけ外部から仕事をされる。
\( W_{CD}=-Q_{out} \)
(エ) 断熱過程なので熱の出入りはなく内部エネルギーの増加分だけ外部から仕事をされる。
\( W_{DA}=\dfrac{3}{2}nR\Delta T=-\dfrac{3}{2}nR(T_{AB}-T_{CD}) \)
(2) 一般に状態1から状態2への等温過程で物質量nの理想気体が外部にする仕事W12は状態1における体積V1、状態2における体積V2、状態1から状態2における絶対温度T12を用いて
\( W_{12}=nRT_{12}\log_e(\dfrac{V_2}{V_1}) \)と表すことができる。ただし\( \log_e \)は自然対数を表す。Qin及びQoutを、それぞれ、n、R、TAB、TCD、VA、VBのうち必要なものを用いて表せ。ここで、VC及び状態Dにおける体積VDは用いないこと。
\( Q_{in}=W_{AB}=nRT_{AB}\log_e(\dfrac{V_B}{V_A}) \)
\( Q_{out}=-W_{CD}=-nRT_{CD}\log_e(\dfrac{V_D}{V_C}) \)となるがVC、VDは使えない。
ここで断熱過程の式から
\( \dfrac{V_C}{V_B}=(\dfrac{T_{AB}}{T_{CD}})^{\dfrac{3}{2}} \)これと同様に
\( \dfrac{V_A}{V_D}=(\dfrac{T_{CD}}{T_{AB}})^{\dfrac{3}{2}} \)片々かけ合わせると、
\( \dfrac{V_C}{V_B}\dot{\dfrac{V_A}{V_D}}=(\dfrac{T_{AB}}{T_{CD}})^{\dfrac{3}{2}}\dot{(\dfrac{T_{CD}}{T_{AB}})^{\dfrac{3}{2}}}=1 \)
\( \dfrac{V_CV_A}{V_DV_B}=1⇨\dfrac{V_DV_B}{V_CV_A}=1 \)
よって\( \dfrac{V_D}{V_C}=\dfrac{V_A}{V_B} \)
以上より
\( Q_{out}=-W_{CD}=-nRT_{CD}\log_e(\dfrac{V_D}{V_C})\\=-nRT_{CD}\log_e(\dfrac{V_A}{V_B})=nRT_{CD}\log_e(\dfrac{V_B}{V_A}) \)
(3) 熱機関Iの熱効率を\( e_{\ I} \)とするとき、\( e_{\ I} \)をTAB、TCDを用いて表せ。
\( e_{\ I}=\dfrac{W_{AB}+W_{BC}+W_{CA}+W_{DA}}{Q_{in}}=\dfrac{Q_{in}-Q_{out}}{Q_{in}}\\=1-\dfrac{Q_{out}}{Q_{in}} \)
\( e_{\ I}=1-\dfrac{nRT_{CD}\log_e(\dfrac{V_B}{V_A})}{nRT_{AB}\log_e(\dfrac{V_B}{V_A})}=1-\dfrac{T_{CD}}{T_{AB}} \)
(大分理系専門塾WINROAD 首藤)