問題

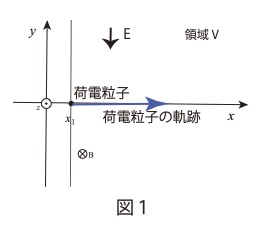
図１のように、紙面上にxy平面、紙面に垂直にz軸を取り、紙面の裏から表への向きをz軸正の向きとする。​\( x>x_1 \)​の範囲を領域Vとし、領域Vにはy軸負の向きで大きさEの一様な電場と、z軸負の向きで磁束密度の大きさBの一様な磁場が加わっている。​\( (x、y、z)=(x_1、0、0) \)​の位置から電気量q(q>0)、質量mの荷電粒子を、x軸正の向きに速さvでxy平面上に射出する。このとき、荷電粒子は電場と磁場による力を受けてx軸上を移動した。荷電粒子は真空中を移動するものとし、領域Vの外では電場及び磁場は０である。また重力の影響は無視する。

(1) 領域V内で荷電粒子が電場から受ける力の大きさを。g、m、n、x1、Eのうち必要なものを用いて求めよ。

(2) 領域V内の磁束密度の大きさBを、q、m、v、x1、Eのうち必要なものを用いて求めよ。

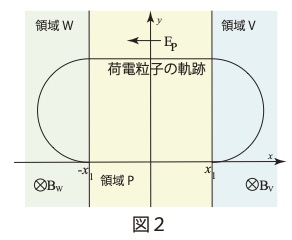
図２のように、​\( x<-x_1 \)​の領域を領域W、​\( -x_1\leqq x\leqq x_1 \)​の領域を領域Pとする。領域Vの一様電場はz軸負の向きで磁束密度の大きさをBvに変更し、電場を０にした。領域Wにはz軸負の向きで磁束密度の大きさをBwの一様な磁場を加え、領域Pにはx軸負の向きで大きさEvの一様な電場を加えた。荷電粒子を​\( (x,\ y,\ z)=(x_1 ,\ 0,\ 0\ ) \)​の位置からx軸正の向きに速さvでxy平面上に射出すると、荷電粒子は図２に太線で示されている軌跡を描いて射出点にもどった。

(3) 領域Vを出てから領域Wに入るまでの間に、領域Pで電場が荷電粒子にした仕事を、q、m、v、x1、Ev

のうち必要なものを用いて表せ。

(4) 一様な電場のの大きさEvをq、m、v、x1、Bv、Bwのうち必要なものを用いて表せ。

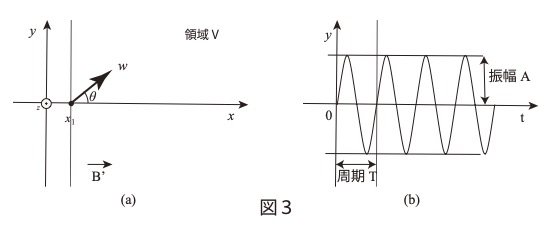
(5) 領域V、P、Wにある全ての磁場と電場を０にした後、図３の(a)のように領域Vにのみx軸正の向きで磁束密度の大きさE’の一様な磁場を加えた。荷電粒子を​\( (x、y、z)=(x_1、0、0) \)​の位置からx軸正の向きとなす角​\( \theta\ (0<\theta<\dfrac{\pi}{2}\ ) \)​の方向へ速さwでxy平面上に射出したところ、荷電粒子のy座標は時刻tに対して図３のようになった。図３の振幅Aと周期Tとして適切なものを、以下の①〜⑧からそれぞれ選べ。なお荷電粒子が射出された時刻を​\( t=0 \)​とする。

① ​\( \dfrac{mw\cos\theta}{qB’} \)​　② ​\( \dfrac{2mw\cos\theta}{qB’} \)​

③ ​\( \dfrac{mw\sin\theta}{qB’} \)​　④ ​\( \dfrac{2mw\sin\theta}{qB’} \)​

⑤ ​\( \dfrac{\pi m}{2qB’} \)​　⑥  ​\( \dfrac{\pi m}{qB’} \)​　⑦ ​\( \dfrac{2\pi m}{qB’} \)​　⑧ ​\( \dfrac{4\pi m}{qB’} \)​

(1) Eにより荷電粒子はy軸負の負の方向にqEの力を受ける。　qE

(2) 荷電粒子は磁場によりy軸正の方向にqvBの力を受ける。荷電粒子が直進したことから(1)の電場による力と磁場による力が釣り合ったので​\( qE=qvB \)​よって​\( B=\dfrac{E}{v} \)​

(3) 荷電粒子は電場Evによる力qEvを受けて2x1の距離を移動したので電場がした仕事は​\( qE_v\times2x_1=2qE_vx_1 \)​となります。

(4) 領域Vを出る時の速さはv、領域Wに入る時の速さをVwとする。

力学的エネルギー保存則より

​\( \dfrac{1}{2}m(V_w)^2=\dfrac{1}{2}mv^2+2qE_Px_1 \)​‥(h)

また領域Vと領域Wでの旋回半径が等しいので、これをrとすると

領域Vでは​\( qvB_v=\dfrac{mv^2}{r}よりr=\dfrac{mv}{qB_v} \)​

領域Wでは​\( qV_wB_w=\dfrac{m(V_w)^2}{r}よりr=\dfrac{mV_w}{qB_w} \)​

よって​\( \dfrac{V_w}{B_w}=\dfrac{v}{B_v}よりV_w=\dfrac{B_w}{B_v}v \)​

(h)より

​\( E_P=\dfrac{m}{4qx_1}(V_w^2-v^2)\\=\dfrac{m}{4qx_1}((\dfrac{B_w}{B_v}v)^2-v^2) \)​

​\( E_P=\dfrac{mv^2}{4qx_1}(\dfrac{B_w^2}{B_v^2}-1) \)​

(5) 領域Vでは荷電粒子の速度wの磁場に垂直な方向の成分​\( w\sin\theta \)​によりz軸の負の方向にローレンツ力を受けてyz平面の方向に円運動を行う。また磁場と同じ方向の速度成分​\( w\cos\theta \)​と相俟って螺旋運動になる。この螺旋半径がAなので​\( q(w\sin\theta)B’=\dfrac{m(w\sin\theta)^2}{A} \)​

よって​\( A=\dfrac{mw\sin\theta}{qB} \)​　　③となります。

​\( T=\dfrac{2\pi A}{w\sin\theta}=\dfrac{2\pi }{w\sin\theta}\cdot \dfrac{mw\sin\theta}{qB}=\dfrac{2\pi m}{qB}\)​　　⑦となります。

（大分理系専門塾WINROAD 首藤）

Follow me!