問題

xy平面上の曲線Cを、媒介変数tを用いて次のように定める。

​\(\small{ x=t+2\sin^2t、y=t+\sin t \quad(0<t<\pi)} \)​

(1) 曲線Cに接する直線のうちy軸と平行なものはいくつあるか求めよ。

(2) 曲線Cのうち​\( \small{y\leqq x }\)​の領域にある部分と直線​\(\small{ y=x} \)​で囲まれた図形の面積を求めよ。

(1) y軸と平行なのでxの増減が変化するところである。

したがって​\( \small{\dfrac{dx}{dt}=1+4\sin t\cos t=1+2\sin 2t} \)​

​\( \small{\dfrac{dx}{dt}=0} \)​とおくと​\( \small{1+2\sin2t=0\\2t=\dfrac{7\pi}{6}\ ,\dfrac{11\pi}{6}\\t=\dfrac{7\pi}{12}\ ,\dfrac{11\pi}{12}} \)​

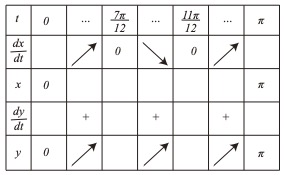
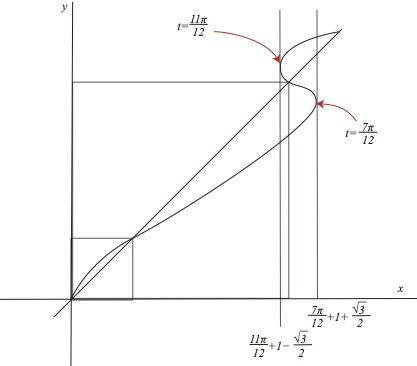
​\( \small{t=\dfrac{7\pi}{12}} \)​のとき

​\( \small{x=t+2\sin^2 t=t+2\cdot\dfrac{1-\cos 2t}{2}\\=t+1-\cos 2t} \)​

なので​\( \small{x=\dfrac{7\pi}{12}+1+\dfrac{\sqrt3}{2}} \)​

​\( \small{t=\dfrac{11\pi}{12}} \)​のとき

​\( x=\dfrac{11\pi}{12}+1-\dfrac{\sqrt3}{2} \)​

​\( \small{\dfrac{dy}{dt}=1+\cos t}>0 \)​

以上より２つ

(2) ​\( y\leqq x \)​なので

​\( t+\sin t\leqq t+2sin^2 t\\2\sin t(\sin t-\dfrac{1}{2})\geqq0\\t=0\ ,\ \dfrac{\pi}{6}\leqq t\leqq \dfrac{5\pi}{6} \)​

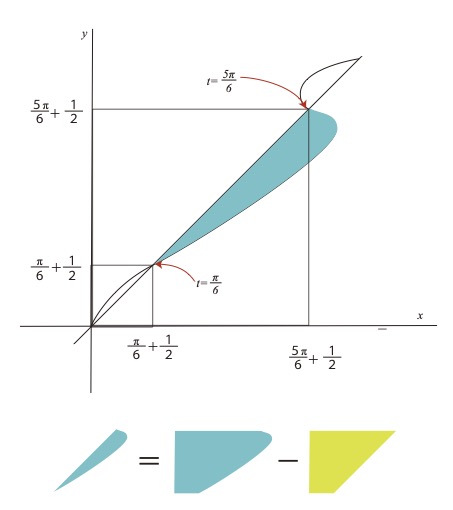
​\( S=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\sin^2 t\ )(1+\cos t\ )dt-\dfrac{1}{2}\{(\dfrac{5\pi}{6}+\dfrac{1}{2})+(\dfrac{\pi}6{}+\dfrac{1}{2})\}\{(\dfrac{5\pi}6{}+\dfrac{1}{2})-(\dfrac{\pi}6{}+\dfrac{1}{2})\} \\=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\sin^2 t\ )(1+\cos t\ )dt-\dfrac{1}{2}\{\pi+1\}\dfrac{2\pi}{3}\\=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\sin^2 t\ )(1+\cos t\ )dt-\dfrac{\pi}{3}(\pi+1)\)​

ここで

​\( \displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\sin^2 t\ )(1+\cos t\ )dt\\=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+t\cos t\ +2\sin^2 t\ +2\sin^2 t\ \cos t)dt\\=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\sin^2 t\ +2\sin^2 t\ \cos t)dt+\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt\\=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\dfrac{1-\cos 2t}{2}\ +2\sin^2 t\ \cos t)dt+\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt\\=\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+1-\cos 2t\ +2\sin^2 t\ \cos t)dt+\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt \)​

​\( \displaystyle\bigl[\dfrac{t^2}{2}+t-\dfrac{\sin 2t}{2}\ +\dfrac{2\sin^3 t}{3}\bigr]_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}+\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt \)​

​\( =\dfrac{1}{2}(\dfrac{25}{36}-\dfrac{1}{36})\pi^2+\dfrac{5\pi}{6}-\dfrac{\pi}{6}-\dfrac{1}{2}(\sin{\dfrac{5\pi}{3}}-\sin{\dfrac{\pi}{3}})+\dfrac{2}{3}(\sin^3{\dfrac{5\pi}{6}-\sin^3{\dfrac{\pi}{6}}})+\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt \\=\dfrac{\pi^2}{3}+\dfrac{2\pi}{3}+\dfrac{\sqrt3}{2}+\displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt\)​

さらに

​\( \displaystyle \int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t\cos t\ )dt\\=\bigl[t\sin t\bigr]_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}\ -\displaystyle \int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(\sin t\ )dt\\=\dfrac{5\pi-\pi}{12}+\bigl[cost\bigr]_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}\\=\dfrac{\pi}{3}-\sqrt3 \)​

なので

​\( \displaystyle\int_{\dfrac{\pi}{6}}^{\dfrac{5\pi}{6}}(t+2\sin^2 t\ )(1+\cos t\ )dt-\dfrac{\pi}{3}(\pi+1)\\=\dfrac{\pi^2}{3}+\dfrac{2\pi}{3}+\dfrac{\sqrt3}{2}+\dfrac{\pi}{3}-\sqrt3-\dfrac{\pi}{3}(\pi+1) \\=\dfrac{2\pi}{3}-\dfrac{\sqrt3}{2}\)​

となります。

考え方は普通ですが計算ミスのないように注意しましょう。

（大分理系専門塾WINROAD 首藤）

Follow me!