今回は単振動でのエネルギー保存則について考えてみましょう。

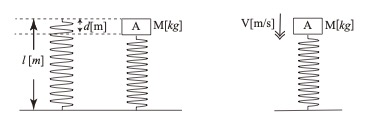
図のように自然長l[m],バネ定数k[N/m]のばねの片方を床に垂直に固定する。

その他端に質量Mの物体Aを取り付ける。このとき、バネはd[m]だけ縮んで

静止した。続いてこの静止した物体Aに下向きに速度V[m/s]を瞬間的に与えた。

次の問いに答えよ。

(1)速度V[m/s]を与えたのち物体Aは最下点に達したのち、単振動を

始めた。最下点の床からの距離を求めよ。

(2)この単振動の周期を求めよ。

解答

(1) 今回２通りの方法で問題を解いてみます。

バネ振り子のエネルギー保存則には次の２通りがあります。

①振動の中心を基準にする場合

Xは振動の中心からの距離

②バネの自然長を基準にする場合

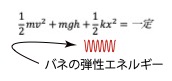
まずは①の方法で解きます。

初めの状態は振動の中心に位置しているので単振動の位置エネルギーは０、

最下点では一旦静止するので運動エネルギーは０となります。

振動の中心から最下点までの距離を Aとおくと

エネルギー保存則①より

これを解くと

したがって床からの距離は

となります。

次に②の方法で解いてみます。

初めの状態は自然長を基準にとると

dだけ縮んでいるので弾性エネルギーは、位置エネルギーはdだけ

下がっているので、運動エネルギーは

最下点の自然長からの距離はxとおくと、

②のエネルギー保存則より

ここで　なので

解の公式で解くと

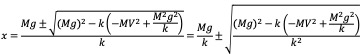
以上より床からの高さは

となり①の場合と同じになります。

このようにどちらの解き方でも解けるのですが、①の方が楽ですよね。

（大分理系専門塾WINROAD 首藤）

Follow me!