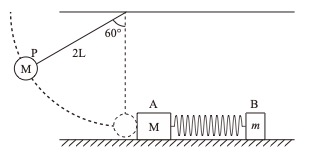
図のように自然長l,バネ定数kの軽いバネの両端に質量Mの物体Aと質量mの物体Bをつけて、
水平で滑らかな床の上におき、全体が静止した状態に、質量M、長さ2Lの単振り子Pを衝突させる。
その後AとBは振動しながら右向きに進んだ。
ただし衝突は完全弾性衝突とする。以下の問いに答えよ。
(1) 衝突直後の物体Aの速度vを求めよ。
以下の問題ではこのvを用いて答えよ。
(2) 重心の速さVGを求めよ。
(3) バネが自然長のとき、重心からBまでの距離を求めよ。
(4) Bの運動は、重心から見たとき単振動となる。この単振動の周期を求めよ。
解答
(1) 衝突直前のPの速度は
力学的エネルギー保存則より
![]()
vについて解くと
![]()
同じ質量かつ完全弾性衝突なので、物体Aの衝突後の速度は
![]()
(2) 今回重心の速さということは物体A,Bをまとめた全体を系として捉えなければならないので
質量Mの振り子が速度vで、質量M+mの系に衝突すると考える。
運動量保存則より
![]()
これにより
![]() となります。
となります。
(別解)
質量Mの物体Aが速度VA,質量mの物体Bが速度VBで運動しているとき重心の速度VGは
![]() となるので、この場合衝突後の物体Aの速度がV,物体Bの速度が0なので
となるので、この場合衝突後の物体Aの速度がV,物体Bの速度が0なので
![]() 今回このA,Bからなる系に外力が働かないので、
今回このA,Bからなる系に外力が働かないので、
重心の速度は一定で変化しない。
よって
![]() となります。
となります。
(3) バネが自然長の時、バネの左端を原点とし重心の位置を求めると
![]()
よって重心から物体Bまでの距離は
![]()
![]() となります。
となります。
(4) 重心から見て物体Bは自然長が![]() のバネの単振動となります。
のバネの単振動となります。
ここで前回の記事の「一様なバネではバネ定数がその長さに反比例する。」
となるのでこの場合のバネ定数Kは
![]() となります。
となります。
よってその周期は
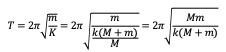 となります。
となります。