以下の問いに答えよ。
(1) 次の3条件(a)、(b)、(c)を満たす整数の組(\( a_1, a_2, a_3, a_4, a_5 \))の個数を求めよ。
(a) \( a_1 \geqq 1 \) 、(b) \( a_5\leqq 4 \) 、(c) \( a_k\leqq{a_{k+1}} \) (k=1 , 2 , 3 , 4 )
(2) 次の3条件(a)、(b)、(c)を満たす整数の組(\( a_1, a_2, a_3, a_4, a_5 \))の個数を求めよ。
(a)\( a_1 \geqq 1 \) 、(b) \( a_k\geqq0 \)( k=2 , 3 , 4 , 5 ) 、(c) \( a_1+a_2+a_3+a_4+a_5\leqq4 \)
(3) n桁の自然数で各桁の数字の合計がr以下となるものの個数をn , r を用いて表せ。
ただし、\( n\geqq1、r\leqq9 \)とする。
(1)
まずこの問題をどう考えよう?
(a),(b)の条件から\( a_1, a_2, a_3, a_4, a_5 \)のいずれも1〜4の数字です。
ここで次のような3つのしきりとボール5つを用意します。
 これを並べ替えたとします。
これを並べ替えたとします。
一例を示します。次のように並んだとします。

これは次のように対応すると考えます。
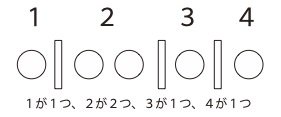
1、2、2、3、4これらを小さいものから順に
\( a_1, a_2, a_3, a_4, a_5 \)にあてていけば良いのです。
このとき\( a_1=1、a_2=2,a_3=2,a_4=3,a_5=4 \)
となります。
ここでもう1例。
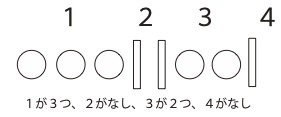
1、1、1、3、3
このとき\( a_1=1、a_2=1,a_3=1,a_4=3,a_5=3 \)
となります。
以上のことから求める個数は\( \dfrac{8!}{3!\cdot5!}=\dfrac{8\cdot7\cdot6}{3\cdot2\cdot1}=56 \)個となります。
(2) 今度は次のように考えます。(1)を参考にしますが条件(a)を考えるとまずボール4つのうち
1つをまず\( a_1 \)に当てておきます。そして条件を次のように考えます
(a)(b)より \( a’_k\geqq0 \)(k=1 , 2 , 3 , 4 , 5)、(c) \( a’_1+a_2+a_3+a_4+a_5\leqq3 \)
そこでしきりを5つとボール3個を用意します。
しきりを5つ用意するのは条件(c)が\( a’_1+a_2+a_3+a_4+a_5\leqq3 \)で\( a’_1+a_2+a_3+a_4+a_5=3 \)では
ないからです。
前回はしきりと数字を、ボールと\( a_1,a_2, a_3, a_4, a_5 \)に対応させていましたが、
今回はしきりと\( a’_1, a_2, a_3, a_4,a_5 \)と対象外を対応させ、ボールの個数を数字に対応させます。
例を示してみます。
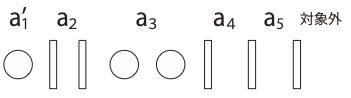
このように並んだとすると
\( a’_1=1, a_2=0, a_3=2, a_4=0, a_5=0 \)となり
結果\( a_1=2, a_2=0, a_3=2, a_4=0, a_5=0 \)
条件については\( a_1=2 \)、\( a_k\geqq0 \)( k=2 , 3 , 4 , 5 )、\( a_1+a_2+a_3+a_4+a_5=4 \)で満たしています
さらにもう一例
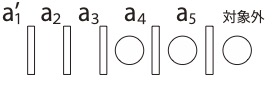
この場合
\( a’_1=0, a_2=0, a_3=0, a_4=1, a_5=1、対象外=1 \)と
なり結果\( a_1=1, a_2=0, a_3=0, a_4=1, a_5=1 \)
条件については\( a_1=1 \)、\( a_k\geqq0 \)( k=2 , 3 , 4 , 5 )、\( a_1+a_2+a_3+a_4+a_5=3 \)で満たしています.
以上のことから求める個数は
\( \dfrac{8!}{5!\cdot3!}=\dfrac{8\cdot7\cdot6}{3\cdot2\cdot1}=56 \)となります。
(3) (2)を参考にするとn桁なので最高位の数から順に\( a_n , a_{n-1}, a_{n-2}, a_{n-3},・・・・・・,a_3, a_2, a_1\)
とすると条件は次のようになります。
(a) \( a_n\geqq1 \)、(b)\( 0\leqq a_k\leqq9 \quad (k=1,2,3\ldots \ldots,n-3,n-2,n-1) \)
(c) \( a_n+a_{n-1}+a_{n-2}+\ldots\ldots+a_3+a_2+a_1\leqq r \)
今回\( r\leqq 9 \)なので(c)で構いません
したがって、しきりをn個(対象外を考えてn個とします。)、ボールを\( r-1 \)個用意して並べ替えます。
以上より求める個数は\( \dfrac{(n+r-1)!}{n!\cdot(r-1)!} \)個となります。
(大分理系専門塾WINROAD 首藤)