鏡がθ回転すると反射光線の回転角は2θ?
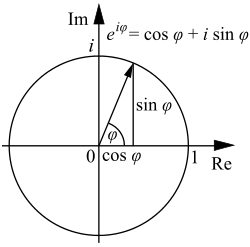
光の速さの測定実験で「フーコーの実験」というものがある。
1850年にフランスの物理学者フーコーは、固定鏡と高速で回転する鏡を用いて光の速さを測定した。
初学段階でよく質問されるのが下記の内容。
「平面鏡がθ回転すると反射光線の回転角は2θになる」
なぜ平面鏡がθ回転すると、反射光線の回転角は2θなるのか??よくわからないという。
簡単ではありますが理由をここに載せておきますね。参考になれば幸いです。
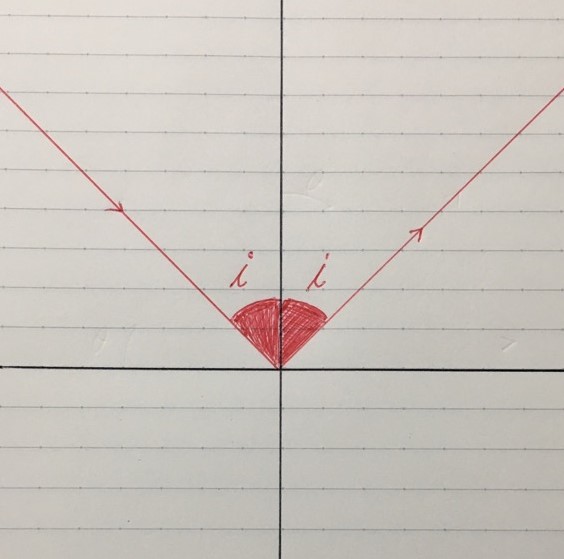
まず最初に確認しておいて欲しいのが「反射の法則」である。
反射面上の入射点に立てた法線と入射射線および反射射線のなす角をそれぞれ入射角、反射角という。
この入射角と反射角の間には「入射角=反射角」つねにが成り立つ。
以上より入射角を「i」とおくと、反射角も「i」となる。
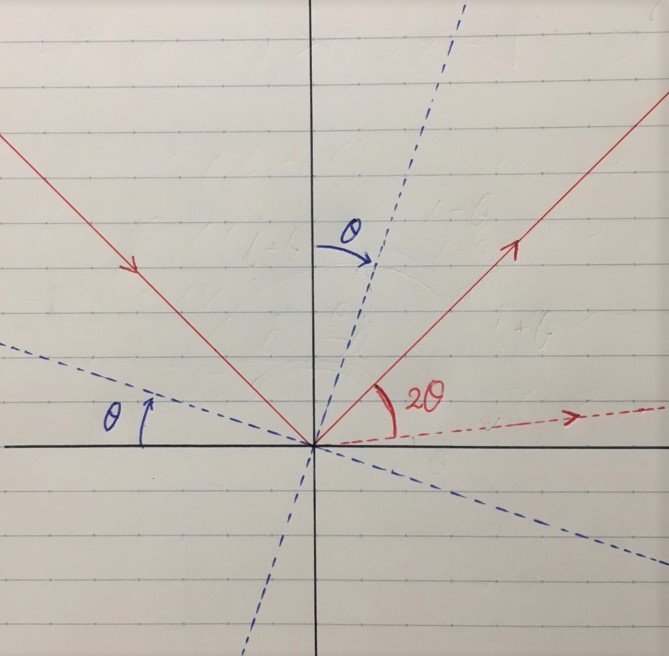
さて、改めて最初の図を見てみよう。

鏡がθだけ回転すると、入射点に立てた法線もθだけ傾くことになる。
法線がθだけ傾くと入射角が変わってきますよね?
当然「反射の法則」から反射角も変わり、赤い実線の反射射線から赤い点線の反射射線に変わる。
以上のことをふまえて図に角度を書き込んでみる。
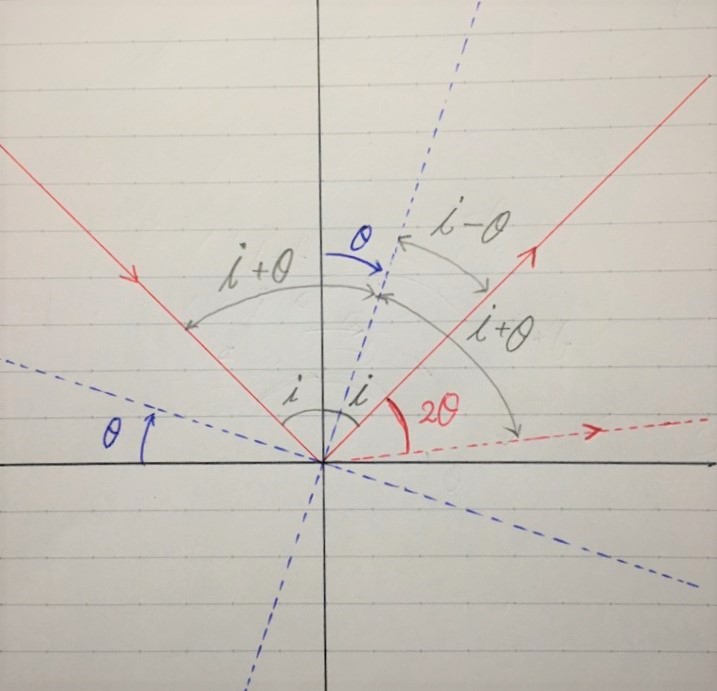
以上より 赤い実線の反射射線と赤い点線の反射射線のなす角をXとすると
X =( i + θ )-( i - θ )= 2θ
となりますね。
イマイチ理解できない人は実際に自分で手を動かして図を書いてみることが大切です。


コメントはありません。