偏差値について(7) 正規分布と偏差値

前回お話しした通り、\(偏差値=\displaystyle\frac{自分の得点-平均点}{標準偏差}✕10+50\) となり、「平均との差」と得点分
布の「バラつきの大きさ」の両方を同時に考えられる指標となっているのが特徴です。これまでは説明
の単純化のため、データの総数(人数)を5や10で行ってきましたが、実際は100人以上のデータ総数で
なければ信頼できる値にはならないことが知られています。また、得点分布が正規分布に近いほど、偏
差値の利用価値が高まります。
一般に偏差値は20~80の間に収まるのですが、理論上は負の値や100を超える値もあり得ます。ただ
その場合は、他の99人が20点以下のテストで1人だけ100点を取ったというくらい極端な、つまり正規
分布に近似できない分布のときです。
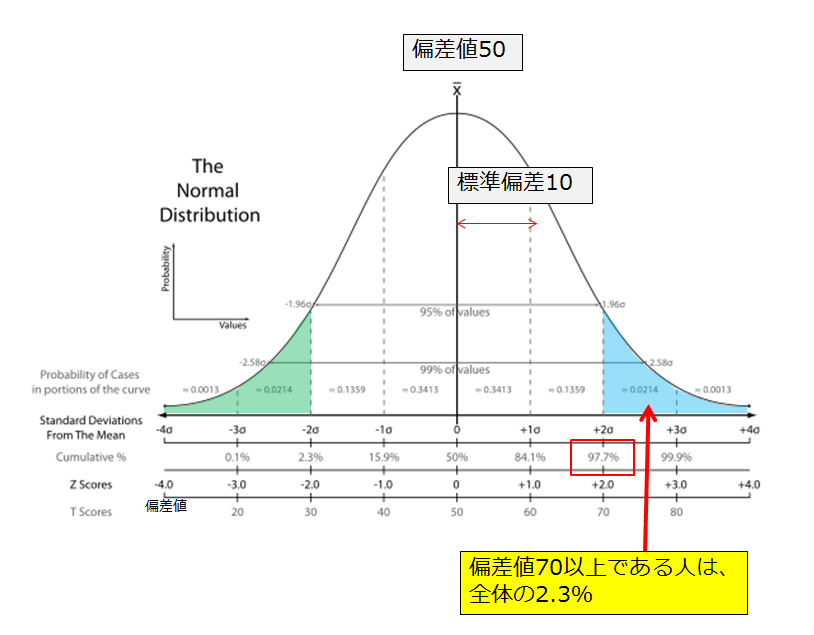
最後に「標準偏差10の正規分布」に近い得点分布での偏差値と順位の対応関係を載せておきます。
| 偏差値 | 順位 | 偏差値 | 順位 |
| 81 | 上位0.1% | 49 | 上位53.98% |
| 80 | 上位0.13% | 48 | 上位57.93% |
| 75 | 上位0.62% | 47 | 上位61.79% |
| 73.3 | 上位1% | 46 | 上位65.54% |
| 70 | 上位2.28% | 45 | 上位69.15% |
| 65 | 上位6.68% | 44 | 上位72.57% |
| 62.8 | 上位10% | 43 | 上位75.80% |
| 60 | 上位15.87% | 42 | 上位78.81% |
| 58 | 上位21.19% | 41 | 上位81.59% |
| 56.8 | 上位25% | 40 | 上位84.13% |
| 56 | 上位27.43% | 39 | 上位86.43% |
| 54 | 上位34.46% | 38 | 上位88.49% |
| 52 | 上位42.07% | 37 | 上位90.32% |
| 51 | 上位46.02% | 36 | 上位91.92% |
| 50 | 上位50% | 35 | 上位93.32% |
尚、上記の偏差値と順位の対応関係をグラフ化したのが前回にも載せた下図です。
文責:金藤


コメントはありません。